Research
Cutting-edge R&D
Our products are based on proprietary in-house research. We run a cutting-edge, multi-disciplinary research team in artificial intelligence (AI) and virtual reality (VR) that not only develops the technologies underlying our products, but also performs fundamental research in these areas. Our research has been published in the top AI and VR venues.
It is our unique multidisciplinary approach, drawing on our backgrounds in physics, computer graphics and vision, applied mathematics, and machine learning, that allows us to bring new insights to solve open problems across these fields.
Scalable and Equivariant Spherical CNNs by Discrete-Continuous (DISCO) Convolutions
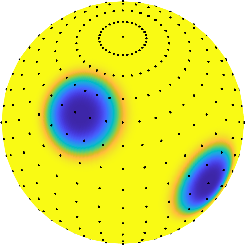
International Conference on Learning Representations (ICLR) (2023)
Abstract: No existing spherical convolutional neural network (CNN) framework is both computationally scalable and rotationally equivariant. Continuous approaches capture rotational equivariance but are often prohibitively computationally demanding. Discrete approaches offer more favorable computational performance but at the cost of equivariance. We develop a hybrid discrete-continuous (DISCO) group convolution that is simultaneously equivariant and computationally scalable to high-resolution. While our framework can be applied to any compact group, we specialize to the sphere. Our DISCO spherical convolutions exhibit SO(3) rotational equivariance, where SO(n) is the special orthogonal group representing rotations in n-dimensions. When restricting rotations of the convolution to the quotient space SO(3)/SO(2) for further computational enhancements, we recover a form of asymptotic SO(3) rotational equivariance. Through a sparse tensor implementation we achieve linear scaling in number of pixels on the sphere for both computational cost and memory usage. For 4k spherical images we realize a saving of 109 in computational cost and 104 in memory usage when compared to the most efficient alternative equivariant spherical convolution. We apply the DISCO spherical CNN framework to a number of benchmark dense-prediction problems on the sphere, such as semantic segmentation and depth estimation, on all of which we achieve the state-of-the-art performance.
Scattering Networks on the Sphere for Scalable and Rotationally Equivariant Spherical CNNs

International Conference on Learning Representations (ICLR) (2022)
Abstract: Convolutional neural networks (CNNs) constructed natively on the sphere have been developed recently and shown to be highly effective for the analysis of spherical data. While an efficient framework has been formulated, spherical CNNs are nevertheless highly computationally demanding; typically they cannot scale beyond spherical signals of thousands of pixels. We develop scattering networks constructed natively on the sphere that provide a powerful representational space for spherical data. Spherical scattering networks are computationally scalable and exhibit rotational equivariance, while their representational space is invariant to isometries and provides efficient and stable signal representations. By integrating scattering networks as an additional type of layer in the generalized spherical CNN framework, we show how they can be leveraged to scale spherical CNNs to the high-resolution data typical of many practical applications, with spherical signals of many tens of megapixels and beyond.
Efficient Generalized Spherical CNNs

International Conference on Learning Representations (ICLR) (2021)
Abstract: Many problems across computer vision and the natural sciences require the analysis of spherical data, for which representations may be learned efficiently by encoding equivariance to rotational symmetries. We present a generalized spherical CNN framework that encompasses various existing approaches and allows them to be leveraged alongside each other. The only existing non-linear spherical CNN layer that is strictly equivariant has complexity O(C2L5), where C is a measure of representational capacity and L the spherical harmonic bandlimit. Such a high computational cost often prohibits the use of strictly equivariant spherical CNNs. We develop two new strictly equivariant layers with reduced complexity O(CL4) and O(CL3 log L), making larger, more expressive models computationally feasible. Moreover, we adopt efficient sampling theory to achieve further computational savings. We show that these developments allow the construction of more expressive hybrid models that achieve state-of-the-art accuracy and parameter efficiency on spherical benchmark problems.
Reducing Cybersickness in 360-Degree Virtual Reality

Multisensory Research, Volume 35, Issue 2 (2021)
[Preprint | PDF | DOI | Product]
Abstract: Despite the technological advancements in Virtual Reality (VR), users are constantly combating feelings of nausea and disorientation, the so called cybersickness. Triggered by a sensory conflict between the visual and vestibular systems, cybersickness symptoms cause discomfort and hinder the immersive VR experience. Here we investigated cybersickness in 360-degree VR. In 360-degrees VR experiences, movement in the real world is not reflected in the virtual world, and therefore self-motion information is not corroborated by matching visual and vestibular cues, which may potentially induce cybersickness. We have evaluated whether an Artificial Intelligence (AI) software designed to supplement the VR experience with artificial 6-degree-of-freedom motion may reduce sensory conflict, and therefore cybersickness. Explicit (questionnaires) and implicit (physiological responses) measurements were used to measure cybersickness symptoms during and after VR exposure. Our results confirmed a reduction in feelings of nausea during the AI supplemented 6-degree-of-freedom motion VR. Through improving the congruency between visual and vestibular cues, users can experience more engaging, immersive and safe virtual reality, which is critical for the application of VR in educational, medical, cultural and entertainment settings.
Technical Blog Posts
For a more accessible introduction to our in-house research, have a look at our related blog posts:

Hyrbid Discrete-Continuous Geometric Deep Learning
Scalable and equivariant spherical CNNs by DISCO convolutions
No existing spherical convolutional neural network (CNN) framework is both computationally scalable and rotationally equivariant. Continuous approaches capture rotational equivariance but are often prohibitively computationally demanding. Discrete approaches offer more favorable computational performance but at the cost of equivariance. We develop a hybrid discrete-continuous (DISCO) group convolution that is simultaneously equivariant and computationally scalable to high-resolution. This approaches achieves state-of-the-art (SOTA) performance on many benchmark dense prediction tasks. Read more on Towards Data Science.

Geometric Deep Learning on Groups
Continuous vs discrete approaches on the sphere
Ideally geometric deep learning techniques on groups would encode equivariance to group transformations, to provide well-behaved representation spaces and excellent performance, while also being computationally efficient. However, no single approach provides both of these desirable properties. Continuous approaches offer excellent equivariance but with a very large computational cost. Discrete approaches are typically relatively computationally efficient but sacrifice equivariance. We point towards future techniques that achieve the best of both worlds. Read more on Towards Data Science.

Scaling Spherical Deep Learning to High-Resolution Input Data
Scattering networks on the sphere for scalable and rotationally equivariant spherical CNNs
Conventional spherical CNNs are not scalable to high resolution classification tasks. In this post we present spherical scattering layers - a novel spherical layer that reduces the dimensionality of the input data while retaining relevant information, while also being rotationally equivariant. Scattering networks work by employing predefined convolutional filters from wavelet analysis rather than learning convolutional filters from scratch. As the weights of scattering layers are designed rather than learned, scattering layers can be used as a one-time preprocessing step that reduces the resolution of the input data. We demonstrate empirically that spherical CNNs equipped with an initial scattering layer can scale to tens of megapixel resolutions, a feat that was previously intractable with conventional spherical CNN layers. Read more on Towards Data Science.
A Brief Introduction to Geometric Deep Learning
AI for complex data
We provide a gentle introduction to geometric deep learning, focusing on high level concepts rather than technical details. We also discuss how spherical AI for 360° data is a particular type of geometric deep learning, falling into the group category. In fact, spherical AI is the canonical example of geometric deep learning on groups, with myriad applications. Read more on Towards Data Science.
Efficient Generalized Spherical CNNs
Hybrid rotationally equivariant spherical CNNs
Notions of spherical convolution offer a promising route to unlocking the potential of deep learning for the variety of problems in which spherical data are prevalent. However, the introduction of non-linearity is a challenge. In this post we explore how ideas originating in quantum physics may be applied to overcome this barrier. We introduce new approaches for implementing these ideas efficiently in practice. Read more on Towards Data Science.

Geometric Deep Learning for Spherical Data
Spherical CNNs
By encoding an understanding of the translational symmetry of the physical world, convolutional neural networks (CNNs) have revolutionised computer vision. In this post we investigate how the principles underlying the success of CNNs may be transferred to the range of problems for which the data exhibits complex geometry, such as the sphere. Read more on Towards Data Science.

Solving Cybersickness with AI
How geometric AI techniques can be used to alleviate cybersickness
While 360° VR can transport you anywhere in the world to enjoy, for example, virtual entertainment, tourism, cultural or educational experiences, today’s technology supports only 3 DOF motion, where you cannot move around in the virtual world. This limits realism and can induce cybersickness. Fortunately, recently developed geometric AI techniques tailored specifically to 360° photos and videos, realised in Kagenova’s copernic360 technology, can synthesise 6 DOF to allow you to move about in the virtual world, alleviating cybersickness and substantially enhancing realism. Read more on Towards Data Science.

What Einstein Can Teach Us About Machine Learning
Harnessing symmetry in machine learning
In many ways physics and machine learning share a common goal: to formulate models of observed phenomena. In achieving this goal physicists have long understood the importance of symmetry. In this post we look at how the ideas of symmetry from physics may be leveraged as guiding principles in machine learning. Read more on Towards Data Science.
Open Source
We make use of and contribute to a number of open source codes developed initially by Kagenova team members.
-
SSHT: Spin spherical harmonic transforms
Functionality to perform fast, exact spin spherical harmonic transforms based on the efficient sampling theory on the sphere of McEwen & Wiaux (2011). -
SO3: Fast Wigner transforms on the rotation group
Functionality to compute fast, exact Wigner transforms on the rotation group based on the efficient sampling theory of McEwen et al. (2015). -
S2LET: Fast wavelets on the sphere
Functionality to compute fast wavelet transforms of signals on the sphere based on the approach outlined in McEwen et al. (2018) and references therein. Axisymmetric, directional and spin wavelet transforms are supported.
Patents
The technology behind our products is patented in a number of juristictions, with further jurisdictions and patents pending.
-
Method and system for providing at least a portion of content having six degrees of freedom motion
-
Configuring an immersive experience
-
Rendering an immersive experience
Related Research
Beyond our work at Kagenova, several team members have done important research in related fields.
Our research programme is led by Prof. Jason McEwen. You can find further details about his research here.
